<단진자와 3차원 벡터>
단진자 운동의 각가속도 벡터로 바꾸는 의미
1. 서론
1. 탐구 동기
2. 단자 운동이란?
단진자(simple harmonic oscillator)란 진동하는 운동을 하는 물체로, 가장 간단한 형태의 진동 운동을 나타낸다. 단진자의 운동은 각속도(angular frequency) ω와 진폭(amplitude) A로 특징지을 수 있으며, 시간 t에 따른 위치 x는 다음과 같은 식으로 나타낼 수 있다.

여기서 phi는 위상(phase)이라고 하며, 초기 조건에 따라 결정된다.
단진자 운동을 나타내는 식에서 각속도 ω를 3차원 벡터(vector)로 바꿔보면 어떻게 될까.
즉, ω를 3차원의 크기와 방향을 가진 물리량으로 생각하면 어떤 의미가 있을까. 이렇게 하면 단진자 운동이 공간에서 어떤 모양으로 진동하는지 알 수 있을 것이다. 이 보고서에서는 단진자 운동의 각속도 ω를 스칼라에서 3차원 벡터로 바꾸는 의미에 대해 설명하도록하겠다.
2. 본론
1. 각속도 벡터의 정의
각속도 벡터는 회전하는 운동을 하는 물체의 회전 속도를 나타내는 물리량이다. 각속도 벡터는 크기와 방향을 가진다. 각속도 벡터의 크기는 단위 시간당 회전하는 각도를 나타내며, 단위는 라디안/초(radian per second)이다. 각속도 벡터의 방향은 오른손 법칙(right-hand rule)에 따라 결정된다. 오른손 법칙이란, 오른손의 네 손가락을 회전 방향으로 휘어주고, 엄지손가락을 펴면, 엄지손가락이 가리키는 방향이 각속도 벡터의 방향이라는 규칙이다.
이러한 점을 이용하여 각속도 벡터를 ω로 나타내면, 다음과 같이 정의된다.

그러면 단진자 운동의 위치 x도 벡터로 나타낼 수 있다.

여기서 A는 각 축 방향의 진폭이고, phi는 각 축 방향의 위상이다.
2. 단진자 운동과 각속도 벡터
단진자 운동을 나타내는 식에서 각속도 ω를 스칼라가 아니라 벡터로 생각하면, 단진자 운동이 공간에서 어떤 모양으로 진동하는지 알 수 있다. 즉, ω의 방향이 단진자가 진동하는 평면의 법선 벡터(normal vector)입니다. 법선 벡터란 평면에 수직인 벡터를 말한다.
이렇게 ω와 x를 벡터로 생각하면 단진자 운동이 공간에서 어떤 모양으로 진동하는지 알 수 있다.
예를 들어

이라면, 단진자 운동은 원점을 중심으로 하는 구면파(spherical wave)로 나타나는 것을 알 수 있다. 즉, 단진자의 위치는 시간에 따라 구면의 표면 위에서 움직인다는 것이다.

반면에,

이라면, 단진자 운동은 원점을 중심으로 하는 원파(circular wave)로 나타난다. 즉, 단진자의 위치는 시간에 따라 원의 표면 위에서 움직인다는 것이다.

또한,
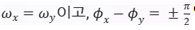
이라면, 단진자 운동은 원점을 중심으로 하는 헬릭스(helix)로 나타난다. 즉, 단진자의 위치는 시간에 따라 나선형으로 움직인다는 것이다.

이렇게 ω와 x를 벡터로 생각하면 단진자 운동에 방향성과 변환성을 부여할 수 있다. 이것은 단진자 운동을 더 잘 이해하고 분석하고 응용할 수 있게 해준다.
4. 일상생활 설명을 통한 각속도 이해(이해를 돕기 위한 ver.)
1. 구면으로 움직이는 경우는 단진자가 세 방향으로 동시에 돌면서, 한 방향으로 계속 이동하지 않는 경우이다. 즉, 단진자는 앞뒤로도 왔다갔다 하고, 좌우로도 왔다갔다 하고, 위아래로도 왔다갔다 하면서, 한 방향으로 가지 않는 경우이다. 예를 들어, 놀이터에서 그네를 타면서, 그네를 좌우로 흔들고, 그네를 앞뒤로 흔들고, 그네를 위아래로 흔들면서, 그네가 앞뒤로 가지 않는 경우, 단진자는 구면으로 움직인다.
2. 원파로 나타나는 경우
단진자 운동이 원으로 움직이는 경우는 단진자가 한 방향으로 돌 때 발생한다. 즉, 단진자가 앞뒤로만 왔다갔다 하거나, 좌우로만 왔다갔다 하거나, 위아래로만 왔다갔다 하는 경우이다. 예를 들어, 놀이터에서 그네를 타면서, 그네를 앞뒤로만 흔들면, 단진자는 원으로 움직인다
3. 나선형으로 도는 경우
단진자 운동이 나선형으로 움직이는 경우는 단진자가 세 방향으로 동시에 돌면서, 한 방향으로 계속 이동하는 경우이다. 즉, 단진자는 앞뒤로도 왔다갔다 하고, 좌우로도 왔다갔다 하고, 위아래로도 왔다갔다 하면서, 한 방향으로 계속 가는 경우이다. 예를 들어, 놀이터에서 그네를 타면서, 그네를 좌우로 흔들고, 그네를 앞뒤로 흔들고, 그네를 위아래로 흔들면서, 그네가 앞으로 계속 가는 경우, 단진자는 나선형으로 움직인다고 볼 수 있다.

단진자가 앞뒤로도 왔다갔다 하고, 좌우로도 왔다갔다 하면서, 두 방향의 각속도가 다를 때 발생하는 것이다. 예를 들어, 놀이터에서 그네를 타면서, 그네를 좌우로 흔들고, 그네를 앞뒤로 흔들면서, 좌우로 흔들 때와 앞뒤로 흔들 때의 각속도가 다르면, 단진자는 8자도 돈다.
8자로 도는 경우는 단진자의 각속도가 두 방향의 각속도를 더한 것이다. 즉, 단진자가 얼마나 빨리 도는지는 두 방향의 각속도를 합쳐서 알 수 있다. 예를 들어, 그네를 타면서, 그네를 좌우로 흔들고, 그네를 앞뒤로 흔들면서, 좌우로 흔들 때와 앞뒤로 흔들 때의 각속도가 다르면, 그네가 얼마나 빨리 도는지는 좌우로 흔들 때의 각속도와 앞뒤로 흔들 때의 각속도를 합쳐서 알 수 있다.
4. 결론
이 보고서에서는 단진자 운동의 각속도 ω를 스칼라에서 3차원 벡터로 바꾸는 의미에 대해 탐구하였다. 우선 단진운동을 벡터로 나타내면 위치와 속도, 각속도를 정확하게 표현 할 수 있다는 장점이 있었으며 이를 통해 단진자 운동이 공간에서 어떤 모양으로 진동하는지 알 수 있었다. 구체적으로, ω의 방향이 단진자가 진동하는 평면의 법선 벡터라는 것을 알게 되었고, 수식과 예시를 통해 ω와 x를 벡터로 나타내면 단진자 운동이 구면파, 원파, 헬릭스, 8자 등 다양한 모양으로 나타날 수 있다는 것을 알게 되었다. 이렇게 ω와 x를 벡터로 생각하면 단진자 운동에 방향성과 변환성을 부여할 수 있으며, 단진자 운동을 더 잘 이해하고 분석하고 응용할 수 있게 해주었다.
'물리' 카테고리의 다른 글
| 물리학실험 주제탐구보고서- 실험의 한계 본질 및 단진자 운동에서의 실험적 오차에 대한 해석(2) (0) | 2024.03.11 |
|---|---|
| 물리학실험 주제탐구보고서- 실험의 한계 본질 및 단진자 운동에서의 실험적 오차에 대한 해석(1) (0) | 2024.03.11 |
| 물리학실험 주제탐구보고서-회전 물체에 토크가 작용하는 경우 어떠한 현상이 발생하는가. (0) | 2024.03.11 |
| 고급물리학 주제탐구보고서-열역학 2법칙과 음식물 부패의 통계적 모델링 (0) | 2024.03.10 |


